Moving average – скользящее среднее

Views: 2474

Скользящая средняя, скользящее среднее (англ. moving average, MA) — общее название для семейства функций, значения которых в каждой точке определения равны среднему значению исходной функции за предыдущий период. Скользящие средние обычно используются с данными временных рядов для сглаживания краткосрочных колебаний и выделения основных тенденций или циклов. Математически скользящее среднее является одним из видов свёртки (определение с вики).

А теперь конкретно о получении среднего значения.

Для чего это необходимо? Если вы выполняете, например, аналоговые измерения, то очень редко можно получить данные без, так называемого шума. Получая данные необходимо отфильтровать шум и получить реально действующее значение параметра. Для этого применяют среднее значение.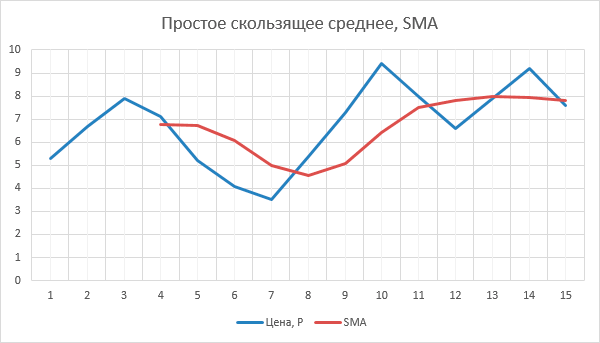

Вычисление среднего.

Как работает вычисление среднего знают все. Для вычисления среднего надо взять N измерений (т.е. взять несколько раз, 5-10-20), затем суммировать и разделить на N (на 5-10-20).

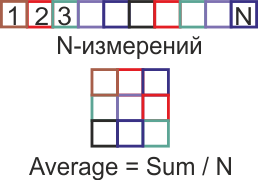Т.е. выполняются последовательно N измерений, за заданное время, после чего всё суммируется и делиться на N полученное значение и есть средняя величина измеряемого параметра.

Недостатком такого вычисление среднего является, то, что для “стабилизации” показаний нужно делать иногда очень много измерений, что естественно приводит к торможению всего процесса изменения. Более того буфер большего объема сжирает память микроконтроллера, что не всегда есть хорошо. Тут и возникает проблема, как бы быстрее измерять, с меньшими ресурсами и получить “стабильные” показания.

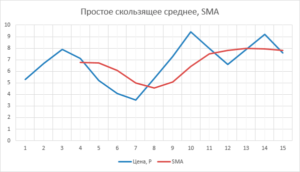
Скользящее среднее.

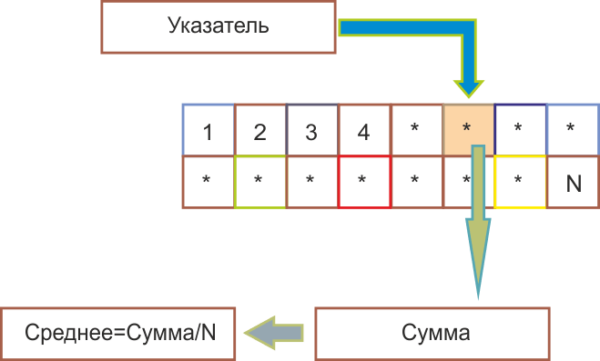
Для этого придумали так называемое скользящее среднее, как это формулах и в математике описывать не будем, тут главное понять сам смысл. Для вычисления скользящего среднего нам так же понадобиться БУФЕР, но естественно на порядок меньшего размера, чем для вычисления обычного математического среднего. Берется отдельно параметр СУММА, который содержит общую сумму данных в буфере, а также мы имеем параметр УКАЗАТЕЛЬ, который будет показывать, с каким данными в буфере выполняются вычисления.

Простое скользящее среднее работает, так:

1. При получении измерения, мы из параметра СУММА вычитаем значение параметра из БУФЕРА на который указывает УКАЗАТЕЛЬ.
2. Полученный параметр, текущего измерения, записываем на место в БУФЕР на который указывает УКАЗАТЕЛЬ.
3. Увеличиваем указатель и проверяем достиг ли он конца БУФЕРА если достиг устанавливаем его в начало.
4. К параметру СУММА прибавляем текущее измерение, а для получения усредненного значения, делим на размер нашего буфера.

Как это все будет выглядеть в Си.

Опишем саму структуру буфера:

// буфер каналов
extern int16_t filtered_data[CHANELES]; // отфильтрованные данные для передачу в программу

// формат данных фильтра скользящее среднее
typedef struct  
{
    int16_t Filter_Data[LEN_FILTER];    // данные фильтра
    int32_t sum;                        // текущая сумма
    int16_t top;                        // указатель на текущую выборку
} __attribute__((packed)) _filter;      // упаковать данные

// определяем масcив данных фильтра
extern _filter filter[CHANELES];        // как внешний

Также не забудем про константы, тут мы должны указать сколько нам таких фильтров нужно и какая глубина фильтра.

// количество фильтров (каналов))
#define CHANELES    9   // количество каналов какой выбрать канал chanll_adapt[]

// константы фильтра для фиксированного варианта и для инициализации варианта с изменяемой глубиной
#define LEN_FILTER  50  // максимальная глубина фильтра

И сама функция вычисления скользящего среднего.

/* фильтр скользящее среднее
 * chanll[a]=Filtering(Get_ADC(), &filter[a]);
 * где  Get_ADC()   данные, например с АЦП
 *      &filter[a]  адрес на начало фильтра 
*/
int16_t Filtering(int16_t input_data, _filter * flt)
{

    flt->sum -= flt->Filter_Data[(int16_t)flt->top];        // отнять от суммы значение на которое указывает top
    flt->Filter_Data[(int16_t)flt->top] = input_data;       // запомнить значение по top
    if(++flt->top > LEN_FILTER-1) flt->top = 0;             // увеличить указатель top, если он больше длины фильтра установить в начало
    return (int16_t)((flt->sum += input_data)/LEN_FILTER);  // к сумме прибавить новое значение и вернуть среднее значение
 
}

Как все это применять. Например, можно в прерывания АЦП вставить строку с функцией или вставить её в основном цикле работы программы:

filtered_data[0]=(int16_t)Filtering(ADC1BUF0, &filter[0]);

В ней данные с АЦП обрабатываются в фильтре с номером 0. И помещаются в буфер отфильтрованных данных, которые можно в дальнейшем использовать для анализа работы или регулировки процесса.

Проблема медленно изменяющего параметра.

Когда параметр медленно изменяется, то в момент дискретизация когда значения находиться межу цифрами, мы можем видеть, то одно, то другое значение. Например, вы сделали спидометр и когда скорость медленно меняется, мы видим “то 7, то 8” и такое “блыманье” часто раздражает. Это можно устранить увеличив глубину фильтра вычисляющего среднее значение, но это приведет так называемой нежелательной “интеграции” параметра визуализации, например скорость уже 100, а показания спидометра медлен нарастают еще несколько секунд. Или вы уже остановись а спидометр еще “Едет”.

Частенько такую проблему решают дискретностью вывода параметра на индикатор, например раз в секунду. На многих индикаторах  (регуляторах) температуры, часто есть такой параметрах, который разрешает обновлять индикация, например, 1 раз в минуту, но это не всегда удобно и практично, а часто и неприемлемо.

Для этого я применяю такой прием, я для него придумал название итерационный фильтр. Суть заключается в том, что поступившие данные сравниваются с предыдущим значением и если значения равны, то счетчик итераций обнуляется. Если же не равны, то начинает работать счетчик итераций и когда достигает заданного значения, новые данные заменяют место старых. Для устранения влияния на работу на больших изменениях параметра, вводиться понятие порога, выше которого данный фильтр неактивен.

Структура данных для фильтра имеет следующий вид:

//------------------------------------------------------------------------------
// формат данных фильтра итераций
typedef struct  
{
     int16_t Data;                  // данные индикации
    uint16_t porog;                 // порог
    uint16_t counter;               // счетчик итераций
    uint16_t counter_set;           // счетчик итераций
} __attribute__((packed)) _fipor;   // упаковать данные

// определяем масcив данных фильтра
extern _fipor fipor[CHANELES];      // как внешний  
//------------------------------------------------------------------------------

Для его работы нужны две функции, инициализации (задания параметров) и сам фильтр.

/* Функция инициализации фильтра */
void InitFilterPor(uint16_t counter_set, uint16_t porog, _fipor * flt);
/* Функция фильтра итераций*/
int16_t FilterPor(int16_t input_data, _fipor * flt);

Использовать следующим образом, сначала инициализация:

    InitFilterPor(20000, 2, &fipor[0]);

Затем в рабочем цикле (или в прерываниях процесса измерения) вставляем фильтр:

FilterPor(calc_temperature (filtered_data[0]), &fipor[0]);

Библиотека с расширенными параметрами, описание в комментах. В этой библиотеке есть расширение которое позволяет использовать скользящее среднее с изменяемыми параметрами в программе, только не забудьте при изменении глубины фильтра необходимо инициализировать указатель, сумму и сам буфер обнулить!!! (смотри описание в библиотеке).

Moving average - скользящее среднее (библиотека V3.0) 3.27 KB 67 downloads

Скользящая средняя, скользящее среднее (англ. moving...

Скачать

Это может быть интересно